2.4.2 Řešené příklady

2.9 Výpočet molární koncentrace roztoku ze zadané hmotnosti rozpuštěné látky a objemu roztoku

Vypočtěte molární koncentraci roztoku hydroxidu sodného o objemu 2 dm³, který vznikl rozpuštěním 80 g NaOH ve vodě.

Řešení:

= 2 dm³

m(NaOH) = 80 g

c(NaOH) = ?

1. postup – úvahou s využitím přímé úměrnosti

víme, že molární koncentrace podle (95) udává počet molů čisté látky (NaOH) rozpuštěné v 1 dm³ roztoku

nejdříve najdeme látkové množství NaOH v 2 dm³ roztoku:

víme, že hmotnost 1 molu NaOH udává jeho molární hmotnost M(NaOH) ≐ 40,00 g⋅mol^-1 můžeme tedy využít úměru (36): 1 mol NaOH..........40,00 g

hledané látkové množství 80 g NaOH můžeme vypočítat užitím přímé úměrnosti:

	1 mol	..................	40 g
	x mol	..................	80 g

x : 1 =	80 : 40
x =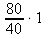
x =	2 moly NaOH ~ n(NaOH) v 2 dm³ roztoku

hledanou molární koncentraci NaOH v 2 dm³ roztoku můžeme podle a. vypočítat užitím přímé úměrnosti:

	2 moly	..................	2 dm³
	x mol	..................	1 dm³

x : 2 =	1 : 2
x =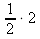
x =	1 mol NaOH c(NaOH) = 1 mol⋅dm^-3

2. postup – postupným dosazováním do jednoduchých vztahů
1. molární koncentrace je definovaná jako (92) – hodnota je zadaná, budeme proto hledat látkové množství rozpuštěného NaOH v roztoku
2. výpočet látkového množství NaOH:
  1. využijeme odvozenývztah (28) pro látkové množství:
  2. do vztahu z A. dosadíme zadanou hodnotu m(NaOH) = 80 g a z tabulek M(NaOH) ≐ 40,00 g⋅mol^-1:
    n(NaOH) = 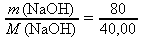= 2 mol
3. do vztahu z a. dosadíme n(NaOH) ≐ 2 mol z b. a zadanou hodnotu = 2 dm³:
  c(NaOH) = 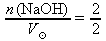= 1 mol⋅dm^-3
3. postup – dosazením do odvozeného vztahu
1. molární koncentrace je definovaná jako (92) – hodnota je zadaná, budeme proto potřebovat jen vztah pro látkové množství rozpuštěného NaOH v roztoku
2. využijeme odvozený vztah (28) pro látkové množství:
3. do vztahu z a. dosadíme vztah z b.:
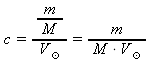
4. do odvozeného vztahu z c. dosadíme zadané hodnoty m(NaOH) = 80 g a
  = 2 dm³ a z tabulek M(NaOH) ≐ 40,00 g⋅mol^-1:
  c(NaOH) = 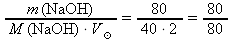= 1 mol⋅dm^-3

Odpověď: Molární koncentrace roztoku NaOH je 1 mol⋅dm^-3 neboli roztok NaOH je 1M.

2.10 Výpočet hmotnosti látky potřebné na přípravu roztoku dané molární koncentrace a objemu

Kolik gramů dusitanu sodného je třeba na přípravu 400 cm³ 4M roztoku této látky?

Řešení:

= 400 cm³

c(NaNO₂) = 4 mol⋅dm^-3

m(NaNO₂) = ? g

1. postup – úvahou s využitím přímé úměrnosti

víme, že molární koncentrace podle (95) udává počet molů čisté látky (NaNO₂) rozpuštěné v 1 dm³ roztoku užitím přímé úměrnosti můžeme vypočítat látkové množství NaNO₂ potřebné na přípravu 400 cm³ = 0,4 dm³ roztoku:

	4 moly	..................	1 dm³
	x mol	..................	0,4 dm³

x : 4 =	0,4 : 1
x =	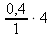= 0,4 ⋅ 4
x =	1,6 mol NaNO₂ ~ n(NaNO₂)

z látkového množství NaNO₂ z a. vypočteme jeho hmotnost:

víme, že hmotnost 1 molu NaNO₂ udává jeho molární hmotnost M(NaNO₂) ≐ 69,00 g⋅mol^-1 můžeme tedy využít úměru (36): 69,00 g...........1 mol NaNO₂

hledanou hmotnost 1,6 molu NaNO₂ můžeme vypočítat užitím přímé úměrnosti:

	69,00 g	..................	1 mol
	x g	..................	1,6 mol

x : 69,00 =	1,6 : 1
x =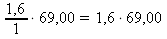
x =	110,40 g NaNO₂ ~ m(NaNO₂)

2. postup – úvahou s využitím přímé úměrnosti

zjistíme, jaké množství NaNO₂ v g bychom museli rozpustit, aby vznikl 4M roztok

víme, že hmotnost 1 molu NaNO₂ udává jeho molární hmotnost M(NaNO₂) ≐ 69,00 g⋅mol^-1 můžeme tedy využít úměru (36): 69,00 g...........1 mol NaNO₂

hledanou hmotnost 4 molů NaNO₂ můžeme vypočítat užitím přímé úměrnosti:

	69,00 g	..................	1 mol
	x g	..................	4 moly

x : 69,00 =	4 : 1
x =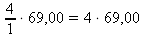
x =	276 g NaNO₂ ~ m(NaNO₂) na přípravu 1 dm³ roztoku

z a. víme, že na přípravu 1 dm³ roztoku je potřeba 276 g NaNO₂ užitím přímé úměrnosti vypočteme kolik g NaNO₂ je potřeba na přípravu 400 cm³ = 0,4 dm³ roztoku:

	276 g	..................	1 dm³
	x g	..................	0,4 dm³

x : 276 =	0,4 : 1
x =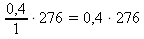
x =	110,4 g NaNO₂ ~ m(NaNO₂) na přípravu 0,4 dm³ roztoku

3. postup – postupným dosazováním do jednoduchých vztahů
1. nejdříve vypočteme látkové množství NaNO₂ potřebné na přípravu roztoku:
  1. využijeme odvozený vztah (93) pro látkové množství:
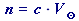
  2. do vztahu z A. dosadíme zadané hodnoty c(NaNO₂) = 4 mol⋅dm^-3 a
    = 400 cm³ = 0,4 dm³:
    n(NaNO₂) = c(NaNO₂) ⋅ = 4 ⋅ 0,4 = 1,6 mol NaNO₂
2. nyní již můžeme určit hmotnost NaNO₂ potřebnou na přípravu roztoku:
  1. využijeme odvozený vztah (27) pro hmotnost:
  2. do vztahu z A. dosadíme n(NaNO₂) = 1,6 mol z a. a z tabulek M(NaNO₂) ≐ 69,00 g⋅mol^-1:
    m(NaNO₂) = n(NaNO₂) ⋅M(NaNO₂) = 1,6 ⋅ 69,00 = 110,4 g NaNO₂
4. postup – dosazením do odvozeného vztahu
1. využijeme odvozený vztah (93) pro látkové množství:
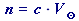
2. dále využijeme odvozený vztah (27) pro hmotnost:
3. vztah z a. dosadíme do vztahu z b.:
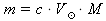
4. do odvozeného vztahu z c. dosadíme zadané hodnoty c(NaNO₂) = 4 mol⋅dm^-3 a
  = 400 cm³ = 0,4 dm³ a z tabulek M(NaNO₂) ≐ 69,00 g⋅mol^-1:
  m(NaNO₂) = 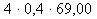= 110,40 g

Odpověď: Na přípravu roztoku je třeba 110,40 gramů dusitanu sodného.

2.11 Výpočet objemu látky a rozpouštědla potřebných na přípravu roztoku dané molární koncentrace a objemu

Kolik cm³ 20% kyseliny sírové (ρ_20% = 1,1394 g⋅cm^-3) a kolik cm³ vody je potřeba na přípravu 1,5 dm³ 2,064M roztoku této látky o hustotě 1,1243 g⋅cm^-3?

Řešení:

w_%(H₂SO₄) = 20 %

ρ_20% = 1,1394 g⋅cm^-3

= 1,5 dm³

c(H₂SO₄) = 2,064 mol⋅dm^-3

= 1,1243 g⋅cm^-3

V(H₂SO₄) = ? cm³

V(H₂O) = ? cm³

nejdříve vypočteme hmotnost čisté (100%) kyseliny sírové potřebné na přípravu roztoku:
1. využijeme odvozený vztah (93) pro látkové množství:
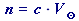
2. dále využijeme odvozený vztah (27) pro hmotnost:
3. vztah z A. dosadíme do vztahu z B.:
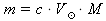
4. do odvozeného vztahu z C. dosadíme zadané hodnoty c(H₂SO₄) = 2,064 mol⋅dm^-3 a = 1,5 dm³ a z tabulek M(H₂SO₄) ≐ 98,08 g⋅mol^-1:
  m(H₂SO₄) = 2,064 ⋅ 1,5 ⋅ 98,08 ≐ 303,66 g 100% kyseliny

roztok však máme připravit ne ze 100%, ale z 20% kyseliny provedeme přepočet

stačí si uvědomit, že hmotnost roztoku kyseliny je nepřímo úměrná jeho procentuální koncentraci (podle (64) a (61) platí: čím více je v roztoku rozpouštědla a tedy i čím větší je hmotnost roztoku, tím je jeho hmotnostní zlomek a koncentrace menší)

hmotnost 20% kyseliny tedy můžeme vypočítat užitím nepřímé úměrnosti:

	303,66 g	..................	100 %
	x g	..................	20 %

x : 303,66 =	100 : 20
x =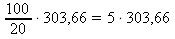
x ≐	1518,3 g ~ m_20% H₂SO₄

hmotnost 20% kyseliny z b. převedeme na objem
1. využijeme odvozený vztah (47) pro objem:
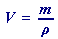
2. do vztahu z A. dosadíme m_20% = 1518,3 g a zadanou hodnotu ρ_20% = 1,1394 g⋅cm^-3:
  V(H₂SO₄) = 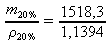= 1332,54 cm³
nyní vypočteme hmotnost vody potřebnou k přípravě roztoku
1. podle (67) platí, že součet hmotností všech látek obsažených v roztoku je roven celkové hmotnosti roztoku, tj. = m_20%(H₂SO₄) + m(H₂O)
2. hmotnost vody lze tedy podle A. vypočítat jako rozdíl hmotnosti roztoku a hmotnosti 20% kyseliny: m(H₂O) = − m_20%(H₂SO₄)
3. vypočteme celkovou hmotnost připravovaného roztoku
  1. využijeme odvozený vztah (48) pro hmotnost:
  2. do vztahu z i. dosadíme zadané hodnoty = 1,2349 g⋅cm^-3 a
    = 1,5 dm³ = 1500 cm³:
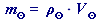    = 1,1243 ⋅ 1500 ≐ 1686,45 g
4. hmotnost vody vypočteme ze vztahu B. dosazením = 1686,45 g z dCii. a m_20% = 1518,3 g z b.:
  m(H₂O) = − m_20%(H₂SO₄) = 1686,45 − 1518,3 = 168,15 g ~ 168,15 cm³ (podle (54))

Odpověď: Na přípravu roztoku je třeba 1332,54 cm³ gramů 20% kyseliny sírové a 168,15 cm³ vody.

2.12 Přepočet molární koncentrace na hmotnostní procenta

Jaká je procentová koncentrace 2,03M roztoku kyseliny dusičné o hustotě 1,0661 g⋅cm^-3?

Řešení:

c(HNO₃) = 2,03 mol⋅dm^-3

= 1,0661 g⋅cm^-3

w_%(HNO₃) = ?

1. postup – úvahou s využitím přímé úměrnosti

abychom mohli potřebné údaje ze známé koncentrace c vypočítat, je třeba zvolit jednu nezávislou veličinu – např. objem roztoku = 1 dm³ (příp. látkové množství n = 1 mol)

vypočteme hmotnost čisté HNO₃ v 1 dm³ roztoku

víme, že molární koncentrace podle (95) udává počet molů čisté látky (HNO₃) rozpuštěné v 1 dm³ roztoku 1 dm³...........2,03 mol
víme, že hmotnost 1 molu HNO₃ udává její molární hmotnost M(HNO₃) ≐ 63,01 g⋅mol^-1 můžeme tedy využít úměru (36): 63,01 g...........1 mol

údaje z A. a B. sestavíme do trojčlenky:

	63,01 g	..................	1 mol
	x g	..................	2,03 mol

x : 63,01 =	2,03 : 1
x =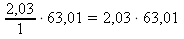
x =	127,91 g HNO₃ ~ m(HNO₃)

vypočteme hmotnost 1 dm³ roztoku
1. využijeme odvozený vztah (48) pro hmotnost:
2. do vztahu z A. dosadíme zadané hodnoty = 1,0661 g⋅cm^-3 a
  = 1 dm³ = 1000 cm³: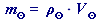
  = 1,0661 ⋅ 1000 ≐ 1066,1 g

vypočteme procentovou koncentraci roztoku

stačí si uvědomit, že hmotnost roztoku je nepřímo úměrná jeho procentuální koncentraci (podle (64) a (61) platí: čím více je v roztoku rozpouštědla a tedy i čím větší je hmotnost roztoku, tím je jeho hmotnostní zlomek a koncentrace menší)

hmotnost HNO₃ (127,91 g) odpovídá 100% roztoku, a proto hmotnostní procento 1066,1 g roztoku můžeme vypočítat užitím nepřímé úměrnosti:

	100 %	..................	127,91 g
	x %	..................	1066,1 g

x : 100 =	127,91 : 1066,1
x =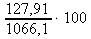
x ≐	12,00 % ~ w_%(HNO₃)

2. postup – postupným dosazováním do jednoduchých vztahů
1. nejdříve si uvědomíme definici procentové koncentrace neboli hmotnostního procenta
  1. využijeme definičních vztahů hmotnostního zlomku látky X v roztoku 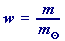(64) a hmotnostního procenta (61)
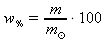
  2. vztah (64) z A. dosadíme do vzahu (61): chceme tedy určit hmotnost čisté kyseliny dusičné m(HNO₃) a hmotnost jejího 2,03M roztoku
2. abychom mohli potřebné údaje ze známé koncentrace c vypočítat, je třeba zvolit jednu nezávislou veličinu – např. objem roztoku = 1 dm³ (příp. látkové množství n = 1 mol)
3. vypočítáme hmotnost čisté kyseliny dusičné m(HNO₃)
  1. využijeme odvozený vztah (93) pro látkové množství:
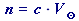
  2. dále využijeme odvozený vztah (27) pro hmotnost:
  3. vztah z A. dosadíme do vztahu z B.:
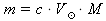
  4. do odvozeného vztahu z C. dosadíme zadanou hodnotu c(HNO₃) = 2,03 mol⋅dm^-3, zvolenou hodnotu = 1 dm³ z b. a z tabulek M(HNO₃) ≐ 63,01 g⋅mol^-1:
    m(HNO₃) = 2,03 ⋅ 1 ⋅ 63,01 ≐ 127,91 g čisté kyseliny
4. vypočteme hmotnost roztoku
  1. využijeme odvozený vztah (48) pro hmotnost:
  2. do vztahu z A. dosadíme zadané hodnoty = 1,0661 g⋅cm^-3 a
    = 1 dm³ = 1000 cm³:
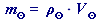    = 1,0661 ⋅ 1000 ≐ 1066,1 g
5. vypočítáme hmotnostní procento roztoku dosazením m(HNO₃) = 127,91 g z c. a
  = 1066,1 g do vztahu z aB.:
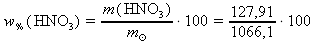  ≐ 12,00 %
3. postup – dosazením do odvozeného vztahu
1. odvození vztahu w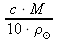_% = pro přepočet molární koncentrace na procentovou koncentraci neboli hmotnostní procenta je mírně složitější, lze jej však vyhledat v literatuře a použít k výpočtu (my ale odvození níže provedeme)
2. nejdříve si uvědomíme definici hmotnostního procenta
  1. využijeme definičních vztahů hmotnostního zlomku látky X v roztoku 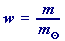(64) a hmotnostního procenta (61)
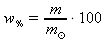
  2. vztah (64) z A. dosadíme do vzahu (61): vyjádříme hmotnost čisté látky m a hmotnost jejího roztoku
3. vyjádření hmotnosti čisté látky m
  1. využijeme odvozený vztah (93) pro látkové množství:
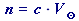
  2. dále využijeme odvozený vztah (27) pro hmotnost:
  3. vztah z A. dosadíme do vztahu z B.:
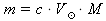
4. vyjádření hmotnosti roztoku
  1. využijeme odvozený vztah (48) pro hmotnost:
  2. vztah z A. přeznačíme, aby se nepletl s hmotností z c.:
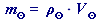
5. do odvozeného vztahu z b. dosadíme odvozené vztahy z c. a z d. a vyjádříme hmotnostní procento ve správných jednotkách (g⋅cm^-3 = kg⋅dm^-3):
  
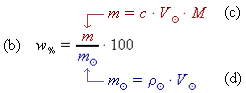
  w_% = =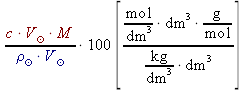
  = =
  = = =
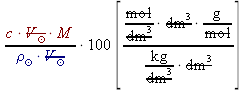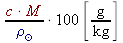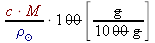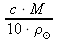
  w_% = ,
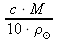  kde w_% ..... procentová koncentrace roztoku (hmotnostní procento).[%]
  c ..... molární koncentrace [mol⋅dm^-3]
  M ..... molární hmotnost [g⋅mol^-1]
  ..... hustota roztoku v [g⋅cm^-3]
6. do odvozeného vztahu z e. dosadíme zadané hodnoty c(HNO₃) = 2,03 mol⋅dm^-3, = 1,0661 g⋅cm^-3 a z tabulek M(HNO₃) ≐ 63,01 g⋅mol^-1:
  w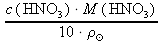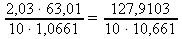_% = = ≐ 12,00 %

Odpověď: Procentová koncentrace 2,03M roztoku kyseliny dusičné je 12,00 %.

2.13 Přepočet hmotnostních procent na molární koncentraci

Jaká je molární koncentrace 30% kyseliny chlorovodíkové o hustotě 1,1493 g⋅cm^-3?

Řešení:

w_%(HCl) = 30 %

= 1,1493 g⋅cm^-3

c(HNO₃) = ?

1. postup – postupným dosazováním do jednoduchých vztahů

abychom mohli potřebné údaje ze známé koncentrace c vypočítat, je třeba zvolit jednu nezávislou veličinu – např. objem roztoku = 1 dm³ (příp. látkové množství n = 1 mol)
vypočteme hmotnost 1 dm³ 30 % roztoku HCl
1. využijeme odvozený vztah (48) pro hmotnost:
2. do vztahu z A. dosadíme zadané hodnoty = 1,1493 g⋅cm^-3 a
  = 1 dm³ = 1000 cm³: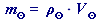
  = 1,1493 ⋅ 1000 ≐ 1149,3 g

vypočteme hmotnost čistého 100% HCl m(HCl) v 30% roztoku

stačí si uvědomit, že hmotnost roztoku je nepřímo úměrná jeho procentuální koncentraci (podle (64) a (61) platí: čím více je v roztoku rozpouštědla a tedy i čím větší je hmotnost roztoku, tím je jeho hmotnostní zlomek a koncentrace menší)

hmotnost 100% HCl tedy můžeme vypočítat užitím nepřímé úměrnosti:

	1149,3 g	..................	30 %
	x g	..................	100 %

x : 1149,3 =	30 : 100
x =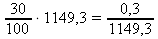
x ≐	344,79 g ~ m(HCl)

vypočteme molární koncentraci HCl m(HCl)
1. molární koncentrace je definovaná jako (92) – objem roztoku jsme v a. zvolili = 1 dm³ c = npotřebujeme jen vypočítat látkové množství rozpuštěného HCl v roztoku
2. využijeme odvozený vztah (28) pro látkové množství:
3. do odvozeného vztahu z B. dosadíme m(NaOH) = 344,79 g z c. a z tabulek M(HCl) ≐ 36,46 g⋅mol^-1:
  n(HCl) = 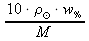= 9,46 mol c(HCl) = 9,46 mol⋅dm^-3

2. postup – dosazením do odvozeného vztahu
1. odvození vztahu w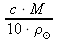_% = pro přepočet molární koncentrace na procentovou koncentraci neboli hmotnostní procenta je mírně složitější, lze jej však vyhledat v literatuře a použít k výpočtu (my ale odvození níže provedeme)
2. nejdříve si uvědomíme definici hmotnostního procenta
  1. využijeme definičních vztahů hmotnostního zlomku látky X v roztoku 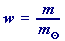(64) a hmotnostního procenta (61)
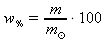
  2. vztah (64) z A. dosadíme do vzahu (61): vyjádříme hmotnost čisté látky m a hmotnost jejího roztoku
3. vyjádření hmotnosti čisté látky m
  1. využijeme odvozený vztah (93) pro látkové množství:
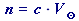
  2. dále využijeme odvozený vztah (27) pro hmotnost:
  3. vztah z A. dosadíme do vztahu z B:
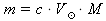
4. vyjádření hmotnosti roztoku
  1. využijeme odvozený vztah (48) pro hmotnost:
  2. vztah z A. přeznačíme, aby se nepletl s hmotností z c.:
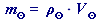
5. do odvozeného vztahu z b. dosadíme odvozené vztahy z c. a z d. a vyjádříme hmotnostní procento ve správných jednotkách (g⋅cm^-3 = kg⋅dm^-3):
  
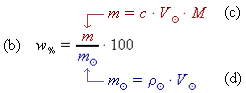
  w_% = =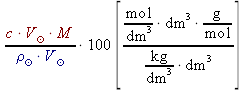
  = =
  = = =
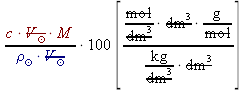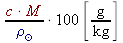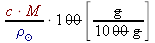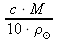
6. z odvozeného vztahu z e. vyjádříme molární koncentraci c:
  w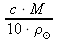_% = ∕ ⋅ 10 ⋅
  10 ⋅ ⋅ w_% = c ⋅ M ∕ : M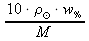
  = c
  c = ,
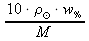  kde c ..... molární koncentrace [mol⋅dm^-3]
  ..... hustota roztoku v [g⋅cm^-3]
  w_% ..... procentová koncentrace roztoku (hmotnostní procento).[%]
  M ..... molární hmotnost [g⋅mol^-1]
7. do odvozeného vztahu z f. dosadíme zadané hodnoty = 1,1493 g⋅cm^-3 a w_%(HCl) = 30 % a z tabulek M(HCl) ≐ 36,46 g⋅mol^-1:
  c(HCl) = 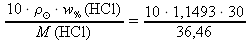≐ 9,46 mol⋅dm^-3

Odpověď: Molární koncentrace 30% kyseliny chlorovodíkové je 9,46 mol⋅dm^-3.

kde	w_%	.....	procentová koncentrace roztoku (hmotnostní procento).[%]
	c	.....	molární koncentrace [mol⋅dm^-3]
	M	.....	molární hmotnost [g⋅mol^-1]
		.....	hustota roztoku v [g⋅cm^-3]

Chemické výpočty

2.4.2 Řešené příklady